Nachdem im ersten Teil einige Catamorphismen vorgestellt wurden, die mit rekursiven Datenstrukturen arbeiten, beschäftigen wir uns nun erstmal mit dem Gegenteil. Ein Anamorphismus verwendet eine CoAlgebra von Typ a -> f a, um eine Datentypen aufzubauen. Damit habe ich es auch eilig, denn ich bin es leid, mir Testdaten stets mühselig im Stile von Node 3 (Leaf (Node 4 Leaf Leaf)) aufzubauen.

Die Coalgebra ist einfach definiert und erklärt:

bulkTreeCoAlgebra :: [Int] -> TreeF [Int]
bulkTreeCoAlgebra [] = LeafF
bulkTreeCoAlgebra xs =
  let (left, x : right) = splitAt (length xs `div` 2) x
   in NodeF x left right

bulkTree :: [Int] -> Tree
bulkTree = ana bulkTreeCoAlgebra

Also im ersten Falle: gegeben eine leere Liste, dann habe ich einen leeren Baum. Und im zweiten Falle: gegeben eine Liste, dann spalte die Liste in 2 halbwegs gleich große Teile und erzeuge einen Node mit dem Mittelelement und den Teillisten.

bulkTree [1..8] ergibt dann diese Teilbaum:

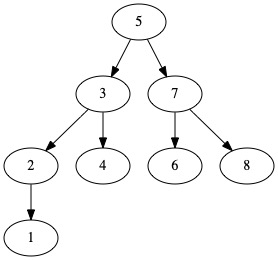
Zygomorphismus

Ein Zygomorphismus beschreibt einen Catamorphismus mit einer zusätzlichen Hilfsalgebra. Nähern wir uns dem Problem langsam an. Wir können bereits die Tiefe eines Baumes berechnen. Nun wollen wir wissen, ob ein Baum balanciert ist. Ein Baum ist balanciert, wenn

• die Teilbäume balanciert sind und
• | Tiefe linker Baum - Tiefe rechter Baum | <= 1 für alle Teilbäume gilt.

Eine klassische rekursive Implementierung mit Hilfe der Funktion go sieht so aus:

balance' :: Tree -> Bool
balance' = snd . go
  where
    go :: Tree -> (Int, Bool)
    go Leaf = (0, True)
    go (Node _ l r) =
      let (ldepth, lbal) = go l
          (rdepth, rbal) = go r
       in (1 + max ldepth rdepth, lbal && rbal && abs (ldepth - rdepth) <= 1)

Zwei Dinge fallen sofort auf, nämlich die explizite Verwendung von Rekursion, und die Wiederholung unserer Implementierung der Berechnung der Tiefe für Leaf 0 und Node (1 + max ldepth rdepth). Das erste Problem haben wir bereits kennengelernt und können es durch die Verwendung eines Catamorphismus umgehen:

balance'' :: Tree -> Bool
balance'' = snd . cata go -- snd gibt das Bool aus dem Tupel zurück
  where
    go :: TreeF (Int, Bool) -> (Int, Bool)
    go LeafF = (0, True)
    go (NodeF _ (ldepth, lbal) (rdepth, rbal)) =
      (1 + max rdepth ldepth, lbal && rbal && abs (ldepth - rdepth) <= 1)

Das zweite Problem lässt sich mit Hilfe eines Zygomorphimus lösen und ermöglicht so auf wundervolle Art und Weise Wiederverwendung von bereits bestehenden Code. Ein Zygomorphismus hat die Struktur : (f b -> b) -> (f (b,a) -> a) -> f -> a.

• f b -> b ist die Hilfsalgebra depthTreeAlgebra :: TreeF Int -> Int, welche wir bereits implementiert haben.
• f (b,a) -> a ist unsere Algebra, die nun sowohl die Tiefe übergeben bekommt, als auch die von uns noch zu implementierende Balanciertheit des Baumes.

Die finale Fassung sieht so aus:

balanceTree :: Tree -> Bool
balanceTree = zygo depthTreeAlgebra zbal
  where
    zbal :: TreeF (Int, Bool) -> Bool
    zbal LeafF = True
    zbal (NodeF _ (ldepth, lbal) (rdepth, rbal)) =
      abs (ldepth - rdepth) <= 1 && rbal && lbal

Epilog

Beim Teutates! Ist das nicht ein bisschen zu viel des Guten? So ein kleiner Algorithmus und so viel Morphismus. Das hätte meine Oma auch programmiert… Stimmt natürlich. Unsere Datenstruktur Tree ist natürlich auch sehr einfach gestrickt. Bei komplexeren Datenstrukturen wird die Notwendigkeit auf Korrektheit geprüfte Algorithmen wiederwenden zu können viel größer. Unsere Morphismen sind ein Handwerkszeug dazu. Und diese kleine Blogserie eine Einladung sich mit diesen Thema auseinanderzusetzen. Also bleibt gespannt: es wird weitergehen…

Archiv

Alle Blogposts zum Thema: Recursion Schemes.

Copyrights

Blog Post Titel Bild (Sierpinsky - Kurve): Beojan Stanislaus, CC BY-SA 3.0