This is part 2 in a series of blog posts on macro metaprogramming in Scala 3. (Click here for part 1) In the previous part I have introduced the two macro APIs as well as several related concepts of metaprogramming with type families and implicits. If you haven’t read it already, you should do so now as the rest of the article won’t be understandable without it. In this second part, we will apply all our knowledge to a practical example and learn how to generate new classes with macros. Quite a bit of arcane magic is necessary to make this possible and it is my goal of this blog series to share with you all the tricks that I have worked out to maneuver around limitations of the compiler.
Motivating example #
As an illustrative example, we will try to generate “case classes” of a special shape from existing case classes:
case class User(name: String, age: Int) // existing class
case class UserOf[F[_]](name: F[String], age: F[Int]) // generated class
The UserOf class that we want to generate is identical to the existing User class, except that every field is wrapped in a type family F[_]. Classes of this shape are commonly called “higher-kinded data”. They appear in many places, for instance UserOf[Option] could be a User form that is partially filled out. The merits of higher-kinded data are beyond the scope of this blog post and irrelevant, but they will make a nice, simple example; deceptively simple perhaps.
Masquerading as a class #
As mentioned previously, it is impossible to generate new symbols with macros that are visible to the user, be it functions, variables or classes. Neither can we generate new classes, nor add methods to existing class bodies. The blog post could be over right here; it is fact and there really is no way around it. However, what we can do is make an existing type act as if it were something else and decorate it with new functionality dynamically, to achieve a very similar user experience as if we had generated a new class from scratch. Scala offers a lot of ways to extend classes with new behaviour without resorting to inheritance such as extension functions, typeclass instances, unapply-functions, typetests and so on, many of which can be combined with macros by a resourceful programmer. The three key ingredients are: structural refinements, dynamic invocations and transparent inline defs.
Structural Refinements #
Refinements are a way to add type information about member variables, member functions or member types to a type reference.
def foo(bar: Bar { val c: Int })
Here we require bar to be of type Bar but also have a field c: Int. Refinements are essentially intersections of types. They narrow the type to a smaller set of values. Importantly, the subtyping of refinements is structural whereas classes are nominally typed. What does this mean? Take the following two classes:
case class Foo(a: Int)
case class Bar(a: Int)
In a nominally typed system Foo and Bar are unrelated despite being structurally identical (they have the same fields). In a nominal type system, subtyping relationships are determined by name, i.e. by an explicit extends declaration, regardless of whether two types are compatible with respect to their fields or runtime representation. Refinements on the other hand are structural in nature and they are subtypes if they have compatible fields no matter the name of the refined type.
We will be using structural refinements to “add fields” to some abstract type with a macro.
Dynamic Invocation #
Structural refinements are intimately related to the two traits scala.Selectable and scala.Dynamic. They are almost identical marker traits that enable a compiler feature to resolve member accesses dynamically. Usually, all accesses of member variables or member functions must be known statically. If the compiler doesn’t know how to access the object’s member at compile time, then it’s a compile error:
class Foo() {}
val foo = new Foo()
foo.a // <--- ERROR: Foo doesn't have a field 'a'
Selectable and Dynamic allow the compiler to translate such a member access to a dynamic method call that is resolved at runtime. The example illustrates how this feature can be used to implement a dynamically typed object like you would have in JavaScript:
class DynamicRecord(fields: (String, Any)*) extends Dynamic {
private val fieldsMap: Map[String, Any] = fields.toMap
def selectDynamic(name: String): Any = fieldsMap(name)
}
val obj: DynamicRecord = DynamicRecord("a" -> 123)
obj.a // resolved to obj.selectDynamic("a") --> fieldsMap("a")
obj.b // resolved to obj.selectDynamic("b") --> compiles but fails at runtime. No entry with key "b".
When an object extends Dynamic, all member accesses are allowed at compile time, even if the class doesn’t have such a field. These member variable accesses are then translated to selectDynamic calls where we can throw an exception at runtime. Since the fields are in a Map, we do not know at compile-time what fields the DynamicRecord will have; it can only be checked at runtime.
Beyond selectDynamic for dynamic fields, we can also implement applyDynamic and applyDynamicNamed to implement dynamically resolved method invocations with or without named parameters:
class Foo() extends Dynamic {
/* dynamically implemented method:
def increment(x: Int) = x + 1
*/
def applyDynamic(methodName: String)(args: Any*): Any = {
(methodName, args) match
case ("increment", Seq(x: Int)) => x + 1
case ("increment", _) => throw NoSuchMethodError(s"Wrong number of arguments")
case _ => throw NoSuchMethodError(s"No method with name $methodName")
}
def applyDynamicNamed(methodName: String)(argsWithNames: (String, Any)*): Any
(methodName, argsWithNames) match
case ("increment", Seq(("x", x: Int)) => return x + 1
case ("increment", Seq((argName, x: Int)) => throw NoSuchMethodError(s"Method doesn't have a parameter $argName")
case ("increment", _) => throw NoSuchMethodError(s"Wrong number of arguments")
case _ => throw NoSuchMethodError(s"No method with name $methodName")
}
val foo = new Foo()
foo.increment(2) // resolved to applyDynamic("increment")(2) --> 3
foo.increment(x = 2) // resolved to applyDynamicNamed("increment")(("x", 2)) --> 3
foo.increment(y = 2) // resolved to applyDynamicNamed("increment")(("y", 2)) --> NoSuchMethodError
foo.increment() // resolved to applyDynamic("increment")() --> NoSuchMethodError
foo.decrement(3) // resolved to applyDynamic("decrement")() --> NoSuchMethodError
Selectable #
The difference between Selectable and Dynamic is that Dynamic will always allow us to call any method or field without compile errors, then will fail at runtime if they’re not implemented. Selectable will only allow us to call a dynamic field/method in the first place, if the object’s type has a structural refinement which asserts that such field/method exists. The invocations are still dynamically resolved (it may still fail at runtime if our refinement lied). Compare this definition of SelectableRecord extends Selectable with the example DynamicRecord extends Dynamic from above:
class SelectableRecord(fields: (String, Any)*) extends Selectable {
private val fieldsMap: Map[String, Any] = fields.toMap
def selectDynamic(name: String): Any = fieldsMap(name)
}
val obj: SelectableRecord { val a: Int } =
SelectableRecord("a" -> 123).asInstanceOf[SelectableRecord { val a: Int }]
obj.a // resolved to obj.selectDynamic("a") --> fieldsMap("a")
obj.b // COMPILE TIME ERROR: obj doesn't have a field b
In contrast to the previous example, we have to add a refinement with {val a: Int} to be able to access a and accessing b will cause a compile-time error instead of a runtime error.
This requirement to have refinement type information about dynamic fields gives Selectable a lot more compile-time safety than Dynamic. However, this is of little concern to us because Dynamic.selectDynamic and Dynamic.applyDynamic can be implemented with def-macros:
class Foo {
inline def applyDynamic(methodName: String)(inline args: Any*): Any = ${ applyDynamicImpl($methodName)($args) }
}
// must be public due to compiler bug
def applyDynamicNamedImpl(methodName: Expr[String])(args: Expr[Seq[Any]]): Expr[Any] = {
if (methodName.valueOrAbort != "increment")
throw NoSuchMethodError(s"No method with name ${methodName.valueOrAbort}")
args match
case '{ $x: Int } => '{ x + 1 }
case _ => throw NoSuchMethodError(s"Wrong argument count or types")
}
Since the applyDynamic macro is executed at compile-time and has access to method name, parameter types, etc. we can check those at compile-time inside the macro. Any exception thrown will result in a compilation error. This way, we get all the flexibility of Dynamic without having to give up compile-time safety. Nonetheless, having a type refinement is still useful to aid with code-completion.
Another difference between Dynamic and Selectable is that Selectable does not have selectDynamicNamed and thus can not implement methods with named arguments, for some unknown reason.
Transparent inline #
Seeing the Any return type of selectDynamic, you may ask yourself: “How can I make the return type depend on the field name?”. Scala 3’s new transparent inline keyword is one way to achieve that. Adding the transparent keyword to an inline method causes the return type of the method to be narrowed to a more specific type than the declared return type after expansion at the callsite, depending on what code-path in the method body is chosen (statically):
inline def foo(b: Boolean): Any =
if b then 1 else "hello"
val x1: Any = foo(true) // x1 == 1 but inferred type is declared Any
val x2: Any = foo(false) // x2 == "hello" but inferred type is declared Any
transparent inline def transFoo(b: Boolean): Any =
if b then 1 else "hello"
val y1: Int = transFoo(true) // x1 == 1 and inferred type narrowed to Int
val y2: String = transFoo(false) // x2 == "hello" and inferred type is narrowed to String
In this case, the inline method’s body is expanded at the callsite and the compiler can statically eliminate the if-expression through constant-folding optimization. What’s left of the inlined method body is either 1 or "hello" and thus the compiler can narrow the return type to Int or String. Of course, narrowing the type can only be performed if a more specific type is actually known at compile time due to use of constants and inline if/inline match.
If the transparent inline method is a macro, this narrowing of the return type can always be performed since the macro is executed at compile time:
class DynamicFoo extends Dynamic {
transparent inline def selectDynamic(name: String): Any = ${ selectDynamicImpl($name) }
}
// must be public due to compiler bug
def selectDynamicImpl(name: Expr[String])(using q: Quotes): Expr[Any] = {
import q.reflect.{*, given}
name.valueOrAbort match
case "a" => '{ 1: Int }
case "b" => '{ 2.34f: Float }
case "c" => '{ "hello": String }
case n => report.errorAndAbort(s"no field named $n", name)
}
// ------- in different file ----------
val foo = DynamicFoo()
val a: Int = foo.a // Any narrowed to Int
val b: Float = foo.b // Any narrowed to Float
val c: String = foo.c // Any narrowed to String
val d = foo.d // COMPILE ERROR: no field named d
A significant drawback of transparent inline methods is that their type-checking relies on inlining (duh) and thus they are subject to ordering problems with other inline methods. As I understand it, inlining in general is never performed within inline methods themselves, but transparent results are only typed after inlining. At the same time, inline functions are type-checked where they are declared and not where they are inlined. If a transparent inline function is called from within another inline function, it will still have its declared type and not the narrowed type when the call-site is type-checked. This means that all our macros relying on transparent inline will plainly not work in inline methods.
Whitebox macros with transparent inline #
Transparent inline methods are “whitebox” in the sense that normally invisible details of the method implementation actually now have an influence on the interface. Callers of the method can “see inside”. If you read part 1 of my articles on macros, all alarms should be going off in your head right now because whitebox macros are exactly the thing we have been searching for. Our regular blackbox macros can alter method bodies however they want and with the help of transparent inline they become grey-ish, being able to essentially generate an arbitrary return type. If we can manage to somehow reference the inferred return type of an inline method, then we have a macro that can generate usable types. We can not write something like ReturnTypeOf[method] unfortunately, neither can we write typeOf[result]. What we can do is reference a member type of the returned value, thus the generated type should be placed in a type member:
class WrappedInOption[T] {
type Out
}
transparent inline given wrapInOption[T]: WrappedInOption[T] = ${ wrapInOptionImpl[T] }
private def wrapInOptionImpl[T: Type](using q: Quotes): Expr[WrappedInOption[T]] =
import q.reflect.{*, given}
'{ (new WrappedInOption[T]).asInstanceOf[WrappedInOption[T] { type Out = Option[T] }] } // imagine a more complicated macro here
In the macro implementation we instantiate an arbitrary class WrappedInOption and then cast it to a refined WrappedInOtion[T] { type Type = ... }. The runtime value of WrappedInOption is completely irrelevant, the only thing that counts is the inferred return type, so it will suffice to cast. The type argument is erased and we only care about the type Out, which only exists on the type-level. Why this roundabout way? Your first instinct is probably to do something like this instead:
'{ new WrappedInOption[T] { override type Out = ??? } }
It will not work, because this is really shorthand for instantiating an anonymous class:
'{
class WrappedInOption$anonClass[T] { override type Out = ??? }
new WrappedInOption$anonClass[T]: Any
}
An anonymous class’s visibility is limited to the local scope; it is not known outside the quotation block and so it is only natural that the inferred return type is actually Any! If you inspect the generated Tree, you will see the : Any type annotation that is inserted at the end. A type refinement exists entirely on the TypeRepr level with no visibility and therefore can be inferred as the return type outside the macro. Besides, we wouldn’t be able to create this Tree dynamically anyway, because we lack the necessary method to create a new Symbol for type aliases.
The “generated” type can now be referenced as a path-dependent type of an implicit:
def foo[A](using w: WrappedInOption[A])(optionalA: w.Out) = ???
Putting it all together #
With the “mise en place” done, let’s put everything together and implement our example use case. Remember that we want to generate a type that is similar to the following case classes:
case class User(name: String, age: Int) // existing class
case class UserOf[F[_]](name: F[String], age: F[Int]) // generated class
Dynamic Field Selection #
We will do this by having a single dynamic type for all source case classes, that acts like entire separate classes depending on the type parameter. If you want to support matching on your generated type (which you probably do), then the dynamic implementation class needs to be hidden behind an opaque type alias (or an abstract member type) for reasons that will become clear later:
opaque type HkdFor[T, F[_]] <: Dynamic = HkdForImpl[T]
private class HkdForImpl[T](elems: (String, Any)*)(using
m: Mirror.ProductOf[T],
tName: TypeName[T]
) extends Product, Dynamic:
type Underlying <: T
private type UnderlyingFields = m.MirroredElemTypes
private type UnderlyingLabels = m.MirroredElemLabels
private val fields = Array.from(elems.map(_._2))
override def equals(that: Any): Boolean = that match
case that: HkdForImpl[?] => (that.fields sameElements this.fields)
case _ => false
override def toString = s"HkdFor[${tName.value}, ?](${fields.mkString(", ")})"
object HkdForImpl:
extension [T](self: HkdForImpl[T])
// This has to be an extension and can not be an instance method due to compiler bug https://github.com/scala/scala3/issues/15413
inline def selectDynamic(name: String)(using m: Mirror.ProductOf[T]): Any = ${ selectDynamicImpl[T]('self, 'name, 'm) }
private def selectDynamicImpl[T: Type](using
q: Quotes)(self: Expr[HkdForImpl[T]], name: Expr[String], m: Expr[Mirror.ProductOf[T]]): Expr[Any] =
import q.reflect.{*, given}
val fieldNames = m match
case '{
type elems <: Tuple;
$m: Mirror.ProductOf[s] { type MirroredElemLabels = `elems` }
} =>
tupleToTypeReprs[elems].map {
case ConstantType(StringConstant(fieldName)) => fieldName
case t => throw AssertionError(s"Expected MirroredElemLabel of ${showType[T]} to be a String constant. " +
s"Was: ${Printer.TypeReprStructure.show(t)}")
}
fieldNames.indexOf(name.valueOrAbort) match
case -1 => report.errorAndAbort(s"No such field: $name", name)
case i => '{ $self.fields(${ Expr(i) }) }
This is all stuff we’ve seen before: A Dynamic class with an untyped array of fields; in the companion object a selectDynamic macro method exists to enable selection of member fields with dot-syntax (e.g. instance.field). The macro method knows what fields the class should have by matching on a quoted Mirror.ProductOf[T] where MirroredElemLabels is a tuple of String & Singleton constants of the field names. Since this is a macro, it is executed at compile-time of the program and will fail with a compilation error if a non-existent field is selected.
Why use Dynamic here instead of Selectable? The reason is that Selectable can not implement dynamic methods with named arguments (Dynamic.applyDynamicNamed). If, at some point, we want to add methods with named arguments to our HkdFor type, for example a copy-method, then we will need Dynamic with its applyDynamicNamed method anyway. Recall that the advantage of Selectable is the type safety it provides, only allowing field selection if the instance has a structurally refined type. If we mix Selectable and Dynamic, then the compiler will always fall back to Dynamic’s selectDynamic if no structurally refined field exists for Selectable to use, making Selectable basically useless. It is better to just use Dynamic from the start and not mix the two.
Type Information for Fields #
Note that in the above snippet, HkdFor.selectDynamic is not transparent and returns Any: While we have successfully prevented people from selecting non-existent fields, all the fields are still untyped and the compiler has no static information what fields our HkdFor has, to be used in code completion. To fix this, we will automatically “decorate” any instance of HkdFor with a structural refinement that contains the appropriate statically typed fields, through an implicit conversion that casts the HkdFor[T, F] to the refined type, i.e. HkdFor[T, F] { val a: F[Int] }:
given applyRefinement[T, F[_]](using
refinementHelper: RefinementHelper[T]
): Conversion[HkdFor[T, F], refinementHelper.Out[F]] = new Conversion {
override def apply(x: HkdFor[T, F]): refinementHelper.Out[F] = x.asInstanceOf[refinementHelper.Out[F]]
}
The target refined type is contained in RefinementHelper.Out. It is generated by a transparent inline given macro, as we have seen before:
class RefinementHelper[T] private ():
// ^ Note: must be a class and not trait, so that it can be instantiated and cast in quoted code without generating
// an anonymous class with its own Symbol that would be remembered by the instance.
/** Contains the refined type generated by the macro for parameters [[T]], [[F]] */
type Out[F[_]] <: HkdFor[T, F]
object RefinementHelper:
/** This function serves to introduce a level of indirection because quoted code can not call the private constructor of
* [[RefinementHelper]], whereas calling private functions seems to work fine.
*/
private def indirectlyCallCtor[T]() = new RefinementHelper[T]
transparent inline given [T]: RefinementHelper[T] = ${ givenRefinementHelperImpl[T] }
private def givenRefinementHelperImpl[T: Type](using q: Quotes): Expr[RefinementHelper[T]] =
import q.reflect.{*, given}
try
???
// For some reason quoted code can not call private ctors, but private functions are a-ok!
'{ RefinementHelper.indirectlyCallCtor[T]().asInstanceOf[RefinementHelper[T] { type Out[F[_]] = ??? }] }
catch
case ex: Throwable =>
// Exceptions during the expansion of given-macros are swallowed and the given ignored unless the right
// compiler flags are set, thus we should always print it, too.
Console.err.println(ex)
throw ex
For the sake of brevity, I have left out the most interesting part: How to actually generate the refined type? Somehow, we need to access the type parameter F[_] inside the generated type, to wrap every field in it. In my first attempt, I tried generating the Tree of an anonymous class extending RefinementHelper, which would give us a reference to F, but we cannot generate Trees with new TypeDefs due to API limitations. Perhaps we can create an anonymous class using quotation with a dummy implementation of type Out[F[_]] and then rewrite the right-hand side of type Out[F[_]], somewhat like this:
val template = '{ new RefinementHelper[T] { type Out[F[_]] = Placeholder } }
val transformed = (new TreeMap {
override def transformStatement(tree: Statement)(owner: Symbol): Statement = tree match
case TypeDef("Out", LambdaTypeTree(List(f @ TypeDef("F", _)), rhs)) => ???
case _ => super.transformStatement(tree)(owner)
}).transformTree(template.asTerm)(Symbol.spliceOwner)
This also doesn’t work out, because the anonymous class will be widened to Any in the macro’s return type. (I’m showing it to you anway, because it is a good trick to have up your sleeve). The problem becomes much easier, once we realize that we don’t actually need to reference F in our generated righthand-side, so long as we can make the righthand side also a type lambda that can be used in a quotation, then simply apply F to the generated lambda. With a trick from part 1 of this blog post series, we can do it:
val outTypeRepr: TypeRepr = ???
type OutGen[F[_]]
given Type[OutGen] = outTypeRepr.asType.asInstanceOf
'{ RefinementHelper.indirectlyCallCtor[T]().asInstanceOf[RefinementHelper[T] { type Out[F[_]] = OutGen[F] }] }
What’s left is generating the right lambda TypeRepr. Realize that type Out[F[_]], when expanded, is really type Out >: Nothing <: [F :> Nothing <: [_$1 :> Nothing <: Any] => Any] => Any, so that is the shape of the TypeRepr that we need to create.
val outTypeRepr = TypeLambda(
List("F"),
boundsFn = _ =>
List(
TypeBounds.upper(TypeLambda(
List("_"), // It would be better to use Symbol.freshName here, but it is still experimental.
boundsFn = _ => List(TypeBounds.empty),
bodyFn = _ => TypeRepr.of[Any]
))),
bodyFn = lambdaF =>
type F[_]
given Type[F] = lambdaF.param(0).asType.asInstanceOf
// Add refinements for case class properties
TypeRepr.of[T].caseFieldsWithTypes.foldLeft(TypeRepr.of[HkdFor[T, F]]) {
case (refinementTypeRepr, (fieldName, fieldTypeRepr)) =>
fieldTypeRepr.asType match
case '[fieldType] => Refinement(refinementTypeRepr, fieldName, TypeRepr.of[F[fieldType]])
}
)
type OutGen[F[_]]
given Type[OutGen] = outTypeRepr.asType.asInstanceOf
'{ RefinementHelper.indirectlyCallCtor[T]().asInstanceOf[RefinementHelper[T] { type Out[F[_]] = OutGen[F] }] }
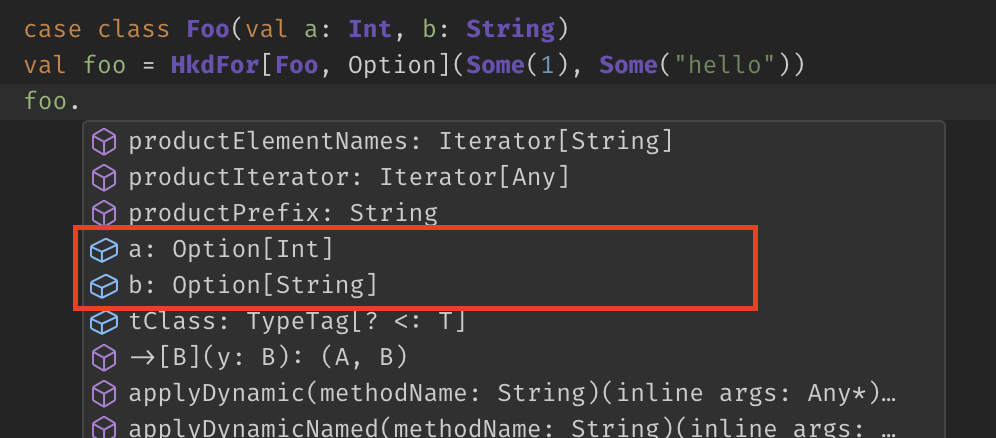
Code completion for structural refinements does not work yet in IntelliJ, only in VSCode.
Constructor and Copy Method #
Next up is creating a constructor and copy method, so that we can create instances of our generated HkdFor type. Since we can not change the constructor of our dynamic implementation class and an opaque type aliases doesn’t have a constructor anyway, a factory method will have to be provided from outside. The way to do this in Scala is to put an apply method in the companion object, which will look just like calling a real constructor. Our constructor should support named arguments, thus we will have a companion object extending Dynamic and implementing Dynamic.applyDynamicNamed:
inline def applyDynamic[T, F[_]](methodName: "apply")(inline args: Any*) =
${ applyDynamicNamedImpl[T, F]('methodName, 'args) }
// noinspection TypeAnnotation
inline def applyDynamicNamed[T, F[_]](methodName: "apply")(inline args: (String, Any)*) =
${ applyDynamicNamedImpl[T, F]('methodName, 'args) }
private def applyDynamicNamedImpl[T: Type, F[_]: Type](
methodNameExpr: Expr[String],
argsExpr: Expr[Seq[Any | (String, Any)]]
)(using q: Quotes): Expr[com.tschuchort.hkd.HkdFor$package.HkdFor[T, F]] =
import q.reflect.{*, given}
val paramNamesTypesValues: Seq[(Option[String], TypeRepr, Expr[Any])] = parseDynamicArgsExpr(argsExpr)
val expectedParamNamesWithTypes = TypeRepr.of[T].caseFieldsWithTypes.map { case (name, typeRep) =>
typeRep.asType match
case '[fieldType] => (name, TypeRepr.of[F[fieldType]])
}
val normalizedParams = checkAndNormalizeParams(
expectedParamNamesWithTypes.map { case (name, tpe) => (name, tpe, /* default */ None) },
paramNamesTypesValues
)
val ctorArgs = Expr.ofSeq(normalizedParams.map { case (name, _, expr) => Expr.ofTuple((Expr(name), expr)) })
val (tMirror, tName) =
Expr.summonAllOrAbort[(Mirror.ProductOf[T], TypeName[T])]
'{
new HkdForImpl[T](${ ctorArgs }*)(using $tMirror, $tClass)
.asInstanceOf[com.tschuchort.hkd.HkdFor$package.HkdFor[T, F]]
// ^ When referencing the fully qualified name of an opaque type, the compiler does not seem to resolve it immediately to
// the RHS even if the opaque type is transparent in this scope. The fully qualified type is "as seen from outside the package".
// Still, the RHS is inferred at the callsite of a transparent def returning an opaque type, but at least with this trick it
// will be recognized as =:= to the opaque type.
}
The code is pretty straight forward, with most of the complexity hidden in utility functions. First we need to parse the arguments expression and disassemble it into separate arguments that we can work with:
def parseDynamicArgsExpr(using q: Quotes)(
argsExpr: Expr[Seq[Any | (String, Any)]],
generalErrorPos: q.reflect.Position = q.reflect.Position.ofMacroExpansion
): Seq[(Option[String], q.reflect.TypeRepr, Expr[Any])] =
import q.reflect.{*, given}
val args = argsExpr match
case Varargs(args) => args
case _ => report.errorAndAbort("Macro internal error: Expected explicit varargs sequence", generalErrorPos)
args.map {
case '{ (${ labelExpr }: String, $valueExpr) } =>
// Widen valueExpr TypeRepr to get rid of Singleton types of String expressions.
// Note: In applyDynamic if some parameters have names and others do not, those
// without names will have the name "" (empty String).
(Some(labelExpr.valueOrAbort).filter(_.nonEmpty), valueExpr.asTerm.tpe.widen, valueExpr)
// "label" -> value;
case '{ ArrowAssoc(${ labelExpr }: String).->(${ valueExpr }) } =>
// Widen valueExpr TypeRepr to get rid of Singleton types of String expressions
(Some(labelExpr.valueOrAbort).filter(_.nonEmpty), valueExpr.asTerm.tpe.widen, valueExpr)
case expr =>
// Widen valueExpr TypeRepr to get rid of Singleton types of String expressions
(None, expr.asTerm.tpe.widen, expr)
}
This is essentially just a rehashing of the Tuple-matching example from part 1.
Next, we need to compute the expected arguments by mapping every field of the source case class T in F (since we expect one argument per field). The only interesting detail here is how to get a TypeRepr from the Symbol of a field because Symbol.caseFields only gives us a list of Symbols and Symbol doesn’t have a method to directly get its TypeRepr, except for Symbol.info which is still experimental. Whenever we are given a Symbol of a member, the TypeRepr of the enclosing parent has to be consulted to find out its TypeRepr because the type of members may depend on type arguments of its parent. TypeRepr.memberType is the method of choice in this case. The result is then wrapped in a TypeIdent to make sure that our TypeRepr is as seen from a global scope:
extension (using q: Quotes)(tpe: q.reflect.TypeRepr)
/** Case class fields zipped with their global TypeRepr */
def caseFieldsWithTypes: List[(String, q.reflect.TypeRepr)] =
import q.reflect.*
tpe.typeSymbol.caseFields.map { symbol =>
(symbol.name, tpe.memberType(symbol).typeSymbol.pipe(TypeIdent.apply).tpe)
}
The main logic of the constructor macro is to check that all the required arguments are there and then pass them on to the HkdForImpl constructor with the right field name. The arguments may be with or without names, in any order, with duplicates or missing arguments. We need to match them to the list of expected fields (expectedParamNamesWithTypes) and then normalize them (put them in the right order and add names where missing). All of this is done in the utility method checkAndNormalizeParams; it is complicated and long, but not very interesting from a macro-perspective, so I will not explain it here any further.
One more interesting tidbit is that we are returning the opaque type HkdFor from the macro. The opaque type is transparent in the scope of the macro implementation (i.e. within the macro, HkdFor is always expanded to HkdForImpl). This can be very problematic because macro methods are always inline and especially if they are transparent inline, the generated code will be expanded at the callsite with opaque types already expanded as if they were still in the defining scope. In other words: all the inlined code will have HkdForImpl instead of HkdFor and the inferred return type of the macro method will be HkdForImpl, leaking implementation details of the opaque type due to a compiler bug. This issue can be partially worked around by always writing the fully qualified name of the opaque type within inline/macro methods. This undocumented feature/bug will make the opaque type be treated “as seen from another package” and somewhat prevent expansion to the RHS. If the macro method is transparent, it will still leak the implementation of the opaque type with this trick, but you will at least get something like HkdFor[T, F] & HkdForImpl[T] as the inferred type instead of just HkdForImpl[T] so that all your other extensions still work (despite inferring HkdForImpl in the IDE, the caller can not actually do anything with that because HkdForImpl is still invisible in the callers scope).
Implementation of the copy method happens analogously to apply. Note that, regrettably., we can not provide any static type information for apply with the refinement trick because copy must have named parameters and those are not supported in structural refinements. You could do something like this to at least provide info on available methods without info on their parameters:
class CopyHelper[T, F](self: HkdFor[T, F]) extends Dynamic {
inline def applyDynamicNamed(methodName: "apply")(args: (String, Any)*): HkdFor[T, F] = ??? // copy implementation here
}
// refinement: HkdFor[Foo, F] { val a: F[Int]; def copy: CopyHelper[T, F] }
Subtype Relationships #
Unless a variance annotation (+T, -T, +F, -F) is used in the definition of opaque type HkdFor[T, F], the HkdFor types will be entirely unrelated to each other. These types are basically case classes and if Cat <: Animal then we definitely also want HkdFor[Cat, F] <: HkdFor[Animal, F]. Otherwise it will not be possible to pass an HkdFor[Cat, F] to a function where HkdFor[Animal, F] is expected, severly hampering its usefulness and sealed traits would be entirely pointless. Adding a variance annotation is the easiest way to establish the subtype relationships, but it is not always possible because the variance annotation may interfere with type inference elsewhere or perhaps there is some relationship you want to establish that is simply more complicated than can be expressed by a variance annotation. As an example of the latter, consider our type parameter F[_]: Clearly we have HkdFor[Foo, Some] { val a: Some[Int] } <: HkdFor[Foo, Option] { val a: Option[Int] } so HkdFor[T, F] should be covariant in F[_]. Because F[_] is a type family, checking F[_] <: G[_] for arbitrary F[_] and G[_] means proving equivalence of μ-recursive functions (theoretically… in practice the recursion of match types is bounded) which would solve the halting problem and is therefore undecidable. The compiler uses simple heuristics to decide if F[_] should be a subtype of G[_], for example a nominal relationship like the one between Some and Option (Some is explicitly declared to extend Option). These heuristics may not be flexible enough for us.
The compiler will not be able to determine equivalence of the following two type families:
type F1[X] = X match
case Int => Int
case Bool => Bool
type F2[X] = X match
case Bool => Bool
case Int => Int
Even more interesting is the following snippet:
case class Foo(a: Int, b: String)
type F3[X] = X match
case Int => Int
case String => String
case Bool => Unit
type F4[X] = X match
case Int => Int
case String => String
case Bool => Nothing
Here F3[_] and F4[_] are clearly not equivalent over the domain of all types, but if we restrict the domain to X <: Int | String, the field types of Foo, then they suddenly are equivalent. In HkdFor[Foo, F], the F[_] will only ever be applied to Int or String, so it would be perfectly safe to assert HkdFor[Foo, F3] =:= HkdFor[Foo, F4].
We, the library programmer, have additional information how the function will be used. Specifically, we know the small finite domain that the function will be called on and we can practically check equivalence more closely than the compiler can, simply by comparing the results of two functions on the few arguments that we care about.
Subtype relationships can be established manually be providing an implicit instance of <:<:
given subtypeWithObviousF[T, S <: T, G[_], F <: [A] =>> G[A]]: (HkdFor[S, F] <:< HkdFor[T, G]) =
scala.<:<.refl.asInstanceOf
This typeclass acts sort of similar to an explicit conversion and will be applied automatically where needed.
Matching / Runtime Type-Tests #
By construction our generated types always differ only in their type arguments, but are supposed to act like completely separate types. It is well known that type arguments get erased at runtime on the JVM. If we want to enable any semblance of useful matching on our generated types, we need to implement runtime type tests manually. Scala 3 offers a new class called TypeTest to do this in an integrated way: if a given TypeTest[A, B] is in scope then the TypeTest.unapply method will be automatically called by the compiler if a match case from A to B can not be checked at runtime by comparing the JVM class only. Matches that can not be checked at runtime include all classes with type parameters (if the match is not for a wildcard), all abstract member types and all opaque types. Unfortunately, the feature is only enabled for the latter two, which is the reason why we introduced the indirection with HkdFor as an opaque type earlier on, instead of exposing the class HkdForImpl directly. A whole array of type tests is necessary to cover all the various cases that can be reasonably checked on HkdFor[T, F], so I will only show one example:
given typeTestDowncastDynamicTComplexF[T, S, F[_], G[_]](using sClass: TypeTag[S])(using
HkdFor[S, G] <:< HkdFor[S, F]
): TypeTest[HkdFor[T, G], HkdFor[S, F]] with {
override def unapply(x: HkdFor[T, G]): Option[x.type & HkdFor[S, G]] =
x match // in this scope we know that HkdFor =:= (HkdForImpl <: Matchable)
case _x: (x.type & HkdForImpl[?]) if (_x.tClass <:< sClass) =>
Some(_x.asInstanceOf[x.type & HkdFor[S, F]])
case _ => None
}
(Note: code must follow this example exactly or the compiler will likely bug out and complain about unassigned type variables)
This type test applies when checking a case _: HkdFor[S, G] for a match scrutinee _: HkdFor[T, F] where S <: T, i.e. a downcast to a more narrow type. A downcast can never be statically checked, thus we need some kind of runtime type information inside HkdForImpl[X] itself to find out what the erased X truly is. To this end, we add a member tClass: TypeTag[X] to the declaration of HkdForImpl[X]:
private class HkdForImpl[+T](elems: (String, Any)*)(using
m: Mirror.ProductOf[T],
tClass: TypeTag[T], // <------- NEW
tName: TypeName[T]
)
For our purposes, TypeTag is simply some abstract type with a <:< method to check if one TypeTag is subtype of another. In place of TypeTag you could use ClassTag from the Scala standard library (with all the limitations outlined in its documentation) or use izumi.reflect.Tag from the third-party izumi-reflect library for a more powerful implementation.
For HkdFor[S, G] <: HkdFor[T, F] to be the case, we must not only have S <: T but also F <: G, roughly speaking. As will be explained later on in the chapter on generic derivation support, we can not add a TypeTag[F] to HkdForImpl here because it would get erased in Mirror.Product.fromProduct(Product): MirroredMonoType. Thus, the relation F <: G must be checkable statically. The Scala compiler can only do this in simple cases, so we delegate the more complicated check to an instance of HkdFor[S, G] <:< HkdFor[S, F] provided elsewhere.
Type-Tests for wildcards #
One more case I want to touch on is wildcards:
x: HkdFor[Foo, Option] match
case _: HkdFor[Foo, ?] => ???
You’d be forgiven to think that wildcards are easier to deal with than concrete types. Wildcards will accept any type after all. One less thing to check. The opposite is the case because we have to be able to provide a TypeTest[Any, HkdFor[T, ?]] in the first place. It turns out that you can write wildcard arguments in a match case, but not in any other place (including a TypeTest declaration): Wildcards can not be applied to an opaque type alias (in contrast to conrete classes where you can always put a wildcard as a type argument). Then how about providing a TypeTest[Any, HkdFor[T, [_] => Any]]? Since a wildcard is essentially Any, that could work. Good idea, but no. It would indeed work, except that there’s not one, but two compiler bugs that foil our plan (I’m starting to see a pattern here): When writing HkdFor[T, ?] the compiler rewrites this to something equivalent to HkdFor[T, Any] despite the fact that the second parameter has kind Type => Type and it is totally illegal to put Any there. Correct would be something like HkdFor[T, [_$1 >: Nothing <: Any] => Any]. Consequently, it is impossible to provide a matching TypeTest because the compiler prohibits us from creating this illegal construct it itself uses. Even with macros that construct the Tree manually I have been unable to circumvent this check and provide a TypeTest for a higher-kinded type with wildcard argument. Maybe someone else has more luck (e-mail me if you find out how).
Matching / Destructuring #
Beyond type ascription based matches, we also want to support destructuring of the type into fields like this:
??? match
case HkdFor[Foo, Option](a: Option[Int], b: Option[String]) => println(s"$a, $b")
This is traditionally done by implementing an unapply method in the companion object and here it is no different. The unapply method, just like apply can be implemented with a def macro or even with applyDynamicNamed, but it is not at all necessary here:
def unapply[F[_]](h: HkdFor[T, F])(using m: Mirror.ProductOf[T]): Tuple.Map[m.MirroredElemTypes, F] =
Tuple.fromProduct(h).asInstanceOf[Tuple.Map[m.MirroredElemTypes, F]]
As you can see, it’s not particularly interesting. The main thing I want to show in this section is how to jump start type inference and how write irrefutable extractors with computed result types. Imagine we want to provide an unapply method that can be used like so, with only one type parameter:
x: HkdFor[?, Option] match
case HkdFor[Foo](a: Option[Int], b: Option[Int]) => ??? // calls HkdFor.unapply[Foo]
Usually, the second parameter F is known statically and fixed (since it can not ever be determined at runtime anyway) and we only want to discriminate on the first parameter, so an unapply method with one parameter would be very useful. This requires that the compiler be able to infer the second parameter correctly. When partial application of multiple type parameters is wanted, the typical approach is to introduce a helper class for indirection:
object HkdFor {
def apply[T]: PartialApplHelper[T]
class PartialApplHelper[T] {
def unapply[F[_]](h: HkdFor[T,F])(using m: Mirror.ProductOf[T]): Tuple.Map[m.MirroredElemTypes, F] =
Tuple.fromProduct(h).asInstanceOf
}
}
x: HkdFor[S, Option] match
case HkdFor[Foo](a: Option[Int], b: Option[Int]) => ??? // expands to HkdFor.apply[Foo].unapply[Inferred]
With this implementation, F[_] =:= Option can be correctly inferred as long as S (the match scrutinee type) is equal to Foo. If, however, S is strictly a supertype of Foo (or unrelated even), then the inferred type for unapply[F[_]] will not be Option but an unknown abstract type F$1 >: [_] =>> Nothing <: [_] =>> Any. The issue here is that the runtime type test for HkdFor[Foo, F$1] can not be performed by the compiler unassissted and so a given TypeTest with its own F[_] parameter is wrapped around the innermost unapply, introducing a level of indrection between the scrutinee HkdFor[S, Option] and the inner pattern binding HkdFor[Foo, F$1]. It seems that the type inference algorithm can not carry the F[_] =:= Option through more than one level of invocations.
We can fix this by writing an extractor definition that does the same work and applies a given TypeTest manually. That way we stay in control of the types:
def unapply[S, F[_]](h: HkdFor[S, F])(using
m: Mirror.ProductOf[T], tt: TypeTest[HkdFor[S, F], HkdFor[T, F]]
): Option[Tuple.Map[m.MirroredElemTypes, F]] =
tt.unapply(h).map { x: HkdFor[T, F] => Tuple.fromProduct(h).asInstanceOf }
This extractor has to be refutable (have an Option[?] result type) as the success of the type test tt is not guaranteed. If you try the code snippet above, you will see that it doesn’t quite work. Instead of destructuring into two variables a: Option[Int], b: Option[Int] the compiler wants us to destructure into a single Tuple:
x: HkdFor[?, Option] match
case HkdFor[Foo]( (a: Option[Int], b: Option[Int]): Tuple ) => ???
But if we write a refutable extractor where the result type tuple is written out manually instead of being Tuple.Map[...] it works fine:
def ExtractBar.unapply(x: Bar): Option[(Int, String)] = ???
x: Bar match
case ExtractBar(a: Int, b: String) => ???
How could this be? In Scala 3 the syntax for unapply-functions (extractors) has been changed. No longer does every unapply-function have to return Option[?]. Instead, there are now several different kinds of unapply-functions which can be looked up here. To summarize:
- Boolean Match:
unapply: Booleanextracts to no bindings (case Bar()) and can fail (when it returnsfalse) - Product Match:
unapply: UwhereU <: ProductandUhas membersval _1: P1; val _2: P2, ... - Optional Match:
unapply: { def isEmpty: Boolean; def get: S }which further divides into:- Optional Single Match:
S <: Anyextracts to a single binding likecase Bar(x: Int) - Optional Name-Based Match:
S <: AnyandShas membersval _1: P1; val _2: P2, ...
- Optional Single Match:
The take-away here is that a Product Match for some reason is always irrefutable and a refutable match (wrapped in Option) always must be either Single Match or Name-Based Match. It appears that Tuple.Map[...] <: Tuple <: Product qualifies as a product match, but once we wrap it in Option, it is no longer allowed to be a Product Match. Neither does Tuple.Map[...] <: Tuple work as a Name-Based Match because it is implemented as a heterogenous typed list (i.e. String *: Int *: EmptyTuple) and so it is forced into a Single Match extracting to a single x: Tuple binding. When a tuple is manually written like Option[(Int, String)] it is translated into Option[Tuple2[Int, String]] which has val _1: Int; val _2: String members and thus qualifies as a refutable Name-Based Match.
Now, can we generate an arbitrary Name-Based Match using macros? No, because the only way to “generate” such a return type would be to make a transparent inline def macro where the return type is narrowed to a structural refinement Any { val _1: Int; val _2: String } but refinements are not considered by the compiler for .Name-Based Match; They have to be real members and not refinements. Perhaps the new named tuples feature released in a future scala version will remedy this problem.
The only possible solution left is to write a macro that creates TupleN[..., ..., ..., ...] types for a fixed N. It only works up to N <= 22, but who is going to write a pattern match with more than 22 fields anyway? An example implementation is provided below:
transparent inline def unapply[S, F[_]](using inline m: Mirror.ProductOf[T])(using tt: TypeTest[HkdFor[S, F], HkdFor[T, F]])(
h: HkdFor[S, F]
): Option[Any] | Boolean = ${ unapplyWithTypeTestImpl[T, S, F]('h, 'tt, 'm) }
private def unapplyWithTypeTestImpl[T: Type, S: Type, F[_]: Type](using q: Quotes)(
h: Expr[HkdFor[S, F]],
tt: Expr[HkdFor[S, F], HkdFor[T, F]]],
m: Expr[Mirror.ProductOf[T]]
): Expr[Option[Any]] | Expr[Boolean] =
import q.reflect.{*, given}
val fieldTypes = m match
case '{
type elems <: Tuple;
$m: Mirror.Product { type MirroredElemTypes = `elems` }
} =>
tupleToTypes[elems].map { case '[field] => TypeRepr.of[F[field]] }
fieldTypes.length match
case 0 => '{ ${ tt }.unapply($h).isDefined }
case l if l <= Tuples.MaxSpecialized =>
type TupleL <: Tuple
given Type[TupleL] = Symbol.classSymbol("scala.Tuple" + l).typeRef
.appliedTo(fieldTypes.toList).asType.asInstanceOf
'{
${ tt }.unapply($h).map { (x: HkdFor[T, F]) =>
Tuples.fromProduct(x).asInstanceOf[TupleL]
}: Option[TupleL]
}
case _ => report.errorAndAbort(s"Only types with 0 to ${Tuples.MaxSpecialized} fields are supported by this extractor", h)
Matching / Exhaustion Checking #
The last thing missing for seamless matching support is exhaustion checking. Normally, the compiler would automatically check for algebraic data types whether the match expression covers all possible cases. With our fake HkdFor type it cannot do it because there is no explicit formal declaration of the set of subtypes. We must find our own way to implement it. The easiest solution would be if we could, somehow, just tell the compiler what subtypes it should check for coverage and then rely on all the existing match checks. Luckily, Scala 3 has a new feature of anonymous union types that we can easily create programatically and yes, they do have exhaustion checking! We just need to cast our base type HkdFor[Base, F] to the union of its subtypes HkdFor[Sub1, F] | HkdFor[Sub2, F] | HkdFor[Sub3, F]:
extension [T, F[_]](self: HkdFor[T, F])(using m: Mirror.SumOf[HkdFor[T, F]])
def asUnionOfCases: Tuple.Union[m.MirroredElemTypes] = self.asInstanceOf
val h: HkdFor[Base, Option] = ???
h.asUnionOfCases match
case HkdFor[Sub1, Option] => ???
case HkdFor[Sub2, Option] => ???
// Missing case Sub3
This approach could be further improved by defining our own match “keyword” that does the casting automatically:
extension [T, F[_], ](self: HkdFor[T, F])(using m: Mirror.SumOf[HkdFor[T, F]])
infix def matchExhaustively[R](f: Tuple.Union[m.MirroredElemTypes] => R): R =
f(self)
h: HkdFor[Base, Option] matchExhaustively {
case HkdFor[Sub1, Option] => ???
case HkdFor[Sub2, Option] => ???
// Missing case Sub3
}
Another compiler bug is once again throwing a wrench into our gears. The above code will fail to compile with the all too familiar “unassigned type variables at the end of typer” message, as long as there are type variables on matchExhaustively that depend on the function f (in this case R). We can work around this by turning it into a transparent inline function, eliminating the need for R:
extension [T, F[_]](self: HkdFor[T, F])(using m: Mirror.SumOf[HkdFor[T, F]])
transparent inline infix def matchExhaustively(inline f: Tuple.Union[m.MirroredElemTypes] => Any): Any =
f(self)
Wouldn’t the world be nice if everything always worked at the first attempt? While the approach from above will indeed enable match exhaustion checking, it will at the same time prevent the compiler from chosing any of the TypeTests we have defined earlier, because they can’t infer HkdFor[Base, F] as the join (least non-union upper bound) of HkdFor[Sub1, F] | HkdFor[Sub2, F] because those types are not officially related to each other. At the same time, writing the type tests to accept arbitrary unions is difficult because the type test similarly needs to find the join of all X <: HkdFor[?, F] in the union to determine F. Depending on how complicated the pseudo-type is that you want to create with your macros, the approach may very well work for you, especially if you can add a covariance annotation (i.e. opaque type HkdFor[+T, F]). Bear in mind that adding the covariance annotation can have unintended consequences on type-inference and choosing of type tests elsewhere.
I elected to instead write my own exhaustion checking macro (for fun). As before, we need to use a transparent inline def to avoid type parameters on the matchExhaustively method:
extension [T, F[_]](self: HkdFor[T, F])
@experimental
transparent inline infix def matchExhaustively(using m: Mirror.SumOf[HkdFor[T, F]])(
inline matchExpression: HkdFor[T, F] => Any
) = ${ matchExhaustivelyImpl[T, F]('self, 'matchExpression, 'm) }
The matchExhaustivelyImpl macro matches on the Tree of the matchExpression lambda to find all case statements. The match itself is pretty hard-coded and fragile; it will fail when slightly different code is generated, but works well enough for this specific case. A better implementation would be to use quotes.TreeAccumulator to be able to match subtrees that are deeply nested in unkown tree elements.
private def matchExhaustivelyImpl[T: Type, F[_]: Type](
self: Expr[HkdFor[T, F]],
expr: Expr[HkdFor[T, F] => Any],
m: Expr[Mirror.Of[HkdFor[T, F]]]
)(using q: Quotes): Expr[Any] =
import q.reflect.{*, given}
val caseDefs = expr.asTerm match
case Inlined(_,
_,
TypeApply(
Select(
Block(
List(
DefDef(
lambdaName,
List(TermParamClause(List(ValDef(lambdaParamName, lambdaParamType, _)))),
_,
Some(Match(matchVar @ Ident(matchVarName), cases))
)
),
Closure(Ident(closureName), _)
),
"$asInstanceOf$"
),
_
)) if closureName == lambdaName && matchVarName == lambdaParamName =>
cases
Next, we got to know what case types to expect. This is done as usual by matching on the Expr[Mirror.Product] and converting the MirroredElemTypes to a list of TypeReprs. (Note that we’re in a transparent function, so any reference to the opaque type HkdFor has to be fully qualified to avoid dealiasing):
def tupleToTypeReprs[T <: Tuple: Type](using q: Quotes): Seq[q.reflect.TypeRepr] =
import q.reflect.{*, given}
Type.of[T] match
case '[head *: tail] => TypeRepr.of[head] +: tupleToTypeReprs[tail]
case '[EmptyTuple] => Seq.empty
val expectedCases: Seq[TypeRepr] = m match
case '{ $m: Mirror.ProductOf[s] } => Seq(TypeRepr.of[com.tschuchort.hkd.HkdFor$package.HkdFor[T, F]])
case '{
type elems <: Tuple;
$m: Mirror.SumOf[s] { type MirroredElemTypes = `elems` }
} =>
tupleToTypeReprs[elems]
The heart of the macro is the following function, which matches on the case defs we gathered earlier to compute the type that it covers:
def computeMatchedType(caseDefPattern: Tree): Seq[TypeRepr] = caseDefPattern match
case Alternatives(patterns) => patterns.flatMap(computeMatchedType)
case TypedOrTest(_, tpt) =>
assert(tpt.symbol.isType)
List(tpt.tpe)
case Bind(bindName, tr) =>
assert(tr.symbol.isType)
List(tr.symbol.typeRef.widenByName)
case Unapply(fun, implicits, bindPatterns) =>
fun.tpe.widenTermRefByName match
// A MethodType is a regular method taking term parameters, a PolyType is a method taking type parameters,
// a TypeLambda is a method returning a type and not a value. Unapply's type should be a function with no
// type parameters, with a single value parameter (the match scrutinee) and with an Option[?] return type
// (no curried function), thus it should be a MethodType.
case methodType: MethodType =>
methodType.resType.asType match
// Also matches Some[] and None in an easy way
case '[Option[tpe]] => TypeRepr.of[tpe] match
case AndType(left, right)
if methodType.paramTypes.nonEmpty && left =:= methodType.param(0) => List(right)
case AndType(left, right)
if methodType.paramTypes.nonEmpty && right =:= methodType.param(0) => List(left)
case tpe => List(tpe)
case '[tpe] => List(TypeRepr.of[tpe])
val caseDefTypes = caseDefs.flatMap { caseDef =>
if caseDef.guard.isDefined then List()
else computeMatchedType(caseDef.pattern)
}
Finally, we can compare the expectedCases to the caseDefTypes to find all expected case that are not covered and emit a warning for them. TypeRepr offers a <:< method to check if one TypeRepr is subtype of another, but that won’t help us much because a HkdFor type is almost never officially a subtype of another HkdFor. We have established most of the subtype relations using given <:< instances, so those will have to be checked as well with Expr.summon:
val uncoveredCases = expectedCases.map(_.asType).filterNot { case '[expectedCase] =>
caseDefTypes.map(_.asType).exists { case '[caseDefType] =>
(TypeRepr.of[expectedCase] <:< TypeRepr.of[caseDefType])
|| Expr.summon[expectedCase <:< caseDefType].isDefined
}
}
if uncoveredCases.nonEmpty then
val casesString = uncoveredCases.map { t => "_: " + Printer.TypeReprCode.show(typeReprOf(t)) }.mkString(", ")
report.warning(
s"Match may not be exhaustive.\n\nIt would fail on case: $casesString",
Position(
self.asTerm.pos.sourceFile,
start = expr.asTerm.pos.start - ("matchExhaustively".length + 1),
end = expr.asTerm.pos.start + 1)
)
Supporting Generic Derivation #
Since our generated types are sort of like case classes, it would be nice if we could make it so that generic derivation in third party libraries, for example generation of JSON codecs, will work with them, too. In part 1 of the blog post, we have touched briefly upon the subject of generic derivation, namely how it depends on information in implicit scala.deriving.Mirror instances. To refresh your memory, a simple example is provided below:
sealed trait Foo[F[_]]
case class Foo1[F[_]](a: F[Int]) extends Foo[F]
case class Foo2[F[_]](b: F[String]) extends Foo[F]
// Mirror.SumOf[Foo[F]]
given [F[_]]: Mirror.Sum with {
type MirroredType = Foo[F]
type MirroredLabel = "Foo"
type MirroredMonoType = Foo[F]
type MirroredElemLabels = ("Foo1", "Foo2")
type MirroredElemTypes = (Foo1, Foo2)
def ordinal(x: MirroredMonoType): Int = x match
case Foo1[?] => 0
case Foo2[?] => 1
}
// Mirror.ProductOf[Foo1[F]]
given [F[_]]: Mirror.Product with {
type MirroredType = Foo1[F]
type MirroredLabel = "Foo1"
type MirroredMonoType = Foo1[F]
type MirroredElemLabels = (a)
type MirroredElemTypes = (F[Int])
def fromProduct(p: Product): MirroredMonoType =
new Foo1[F](p.productElement(0).asInstanceOf[F[Int]])
}
It is also possible to have Mirror instances for partially applied type constructors. In that case, type parameters are added to MirroredType and MirroredElemTypes for the non-applied parameters and MirroredMonoType contains an erased version of the type where the unapplied type parameter is replaced by some upper bound.
// Mirror.ProductOf[[F[_]] =>> Foo[F]]
given Mirror.Product with {
type MirroredType[F[_]] = Foo1[F]
type MirroredLabel = "Foo1"
type MirroredMonoType = Foo1[[_] =>> Any]
type MirroredElemLabels = (a)
type MirroredElemTypes[F[_]] = (F[Int])
def fromProduct(p: Product): MirroredMonoType =
new Foo1[[_] =>> Any](p.productElement(0).asInstanceOf[Any])
}
Importantly, notice that fromProduct returns a newly constructed MirroredMonoType with an erased F and not MirroredType. Since F is not known at this point, it cannot be used in the construction of Foo1. The fromProduct method is used everywhere in libraries (for example Shapeless) to convert back and forth between a generic Tuple and the mirrored class like so:
val foo = Foo1[Option](a = Some(1))
val fooTuple: Tuple1(Option[Int]) = Tuple.fromProduct(foo) // convert Foo1 class to a generic Tuple of fields
val alteredTuple: Tuple1(List[Int]) = Tuple1(fooTuple._1.toList) // do some transformation on a generic Tuple here
val fooAltered: Foo1[List] = summon[Mirror.ProductOf[Foo1]].fromProduct(alteredTuple).asInstanceOf[Foo1[List]] // convert Tuple back to a typed class Foo1
In practice this means for us that, if we want to provide a partially applied Mirror[HkdFor[T, _]], then HkdFor[T, F] must not contain any data depending on F beyond the fields that are listed in MirroredElemTypes because we don’t know what F is when constructing a MirroredMonoType within fromProduct (the MirroredElemTypes may still depend on F because they’re passed in as an untyped argument p: Product from the outside where F is known). We have already run into this problem in the chapter on TypeTests where we were unable to type-test F because no runtime type information on F (like a TypeTag[F]) can be added to HkdForImpl without messing up the Mirror.
These Mirror instances are normally generated by the compiler in-place where they are summoned for algebraic data types (case classes, sealed traits, enums). Normal classes do not have Mirror instances because they don’t have a known finite set of subclasses or are not always trivially constructable from a set of fields. Luckily, Mirror is just a regular typeclass like any other and we can define instances manually if needed. Sounds simple but it can be a little tricky to do because Mirror instances are for the most part just structural refinements of the Mirror interface, with very little runtime behaviour (only the fromProduct/ordinal method). The important part of the Mirror given is its type refinement and not its value. Why is this problematic? After all, we’ve already seen a lot of givens with structural refinement in previous sections. The difference to all our helper classes with refinements is that those helper classes had a type parameter to identify the given and the refinement itself was not involved in implicit search. Remember the helper class we’ve used for adding field information, for example:
class RefinementHelper[T] { type Out[F[_]] <: HkdFor[T, F] }
given applyRefinement[T, F[_]](using RefinementHelper[T]) = ???
The using-clause here is on RefinementHelper[T], identified by T. Never is there a using RefinementHelper[?] { type Ou[F] = FooBar[F] } where {type Out} is the discriminating feature guiding implicit search. Mirror does not have a type parameter and always differs only in the refinement (using Mirror.Of[Foo] expands to using Mirror { type MirroredType = Foo }).
Since Scala 3, the return type of a given/implicit def always needs to be written explicitly and can no longer be inferred. Only this declared type is considered during implicit search. Previously we have relied a lot on transparent inline macros when it came to computing types in a structural refinement, but that won’t work here:
class Foo
transparent inline given Mirror = new Mirror { type MirroredType = Foo }
summon[Mirror { type MirroredType = Foo }] // ERROR: implicit not found
The snippet above will fail with an “implicit not found” error because we’re asking for a Mirror { type MirroredType = Foo } but the declared type of our given is just Mirror. The transparent inline modifier doesn’t help to narrow the type since this type narrowing happens in the inlining phase, i.e. after an implicit has already been chosen and applied. During implicit search, the transparent inferred type of the RHS is unknown.
One way to work around that is to introduce another level of indirection with a helper class. The helper class can then be created by a transparent inline macro, which is inlined and narrowed as the argument to the actual Mirror given:
class Foo
trait Helper {
type Out
val value: Out
}
transparent inline given Helper =
// could be implemented by a macro
new Helper {
type Out = Mirror { type MirroredType = Foo }
val value: Out = new Mirror { type MirroredType = Foo }
}
given (using h: Helper): h.Out /* <: Mirror */ = h.value
summon[Mirror { type MirroredType = Foo }] // works!
Alternatively, if the logic for computing MirroredElemTypes and such is simple enough, we can always try to do everything through type-level programming with Tuples, no macros involved:
inline given [T, F[_]](using m: Mirror.ProductOf[T]): Mirror.Product {
type MirroredType = HkdFor[T, F]
type MirroredMonoType = HkdFor[T, F]
type MirroredLabel = "HkdFor"
type MirroredElemTypes = Tuple.Map[m.MirroredElemTypes, F] // using type function Tuple.Map instead of a macro
type MirroredElemLabels = m.MirroredElemLabels
} = Mirror.Product {
// all the types have to be repeated in declaration and implementation :(
type MirroredType = HkdFor[T, F]
type MirroredMonoType = HkdFor[T, F]
type MirroredLabel = "HkdFor"
type MirroredElemTypes = Tuple.Map[m.MirroredElemTypes, F]
type MirroredElemLabels = m.MirroredElemLabels
override def fromProduct(p: Product): MirroredMonoType = ???
}
This is always a good approach to try first, but from personal experience I want to heavily caution against wasting too much time on type-level programming with Tuples / match types. Dealing with tuple types is a lot like trying to teach a senile old man how to open an e-mail: By the time you get to the e-mail program, he will have already forgotton how to click with the mouse. Similarly, the Scala compiler has a bad tendency to forget the concrete types and widen everything to a generic Tuple, which Tuple.Map can not match on. Hours of trial-and-error are then necessary to find an incantation with inline sprinkled in at just the right places, path-dependent types replaced with Aux-pattern or implicit parameters manually delayed with summonInline, to make it work. Macros look more complicated at first, but are much more reliable and easier to debug.
Shapeless 3 #
One more road block we have to deal with relates to an implementation detail of Shapeless 3. Since Shapeless 3 is one of the primary ways that library authors use to provide generic derivation, it’s imperative that we support it. If you look at the Shapeless source code, you will see that relevant methods do not depend on Mirror directly. Instead, they always depend on Generic, which is the Shapeless analog to Mirror:
inline given mkInstances[F[_], T](using gen: K1.Generic[T]): K1.Instances[F, T]
As explained in part 1 of the blog post, Generic is nothing more than a type refinement of Mirror to make sure every member type has the same kind as the mirrored type:
type K1.Generic[O[_]] = Mirror {
type Kind = K1.type // <---- This is new!
type MirroredType[X] = O[X]
type MirroredMonoType = O[Any]
type MirroredElemTypes[_] <: Tuple
}
Refinement of a type always leads to a new implicit search scope. Clearly, a given Mirror[T] will not fit where a using K0.Generic[T], i.e. using Mirror[T] { type Kind = K0.type } is asked. The problem for us is that there is no given declaration anywhere in Shapeless to go from Mirror –> Generic automatically! Coincidentally, Shapeless still works fine with default Mirrors because the compiler knows that Mirror has the same runtime representation as Mirror { type FooBar = Noxarp } and will happily provide any arbitrary refinement that you ask for, but any manually created custom Mirror instance without the refinement will not be picked up by Shapeless. The take-away is that it is not enough for us to provide Mirror. The declared type of our givens has to be identical to Generic:
inline given [T, F[_]](using m: Mirror.ProductOf[T]): (K0.ProductGeneric & Mirror.Product {
type Kind = K0.type // <------------ NEW
type MirroredType = HkdFor[T, F]
type MirroredMonoType = HkdFor[T, F]
type MirroredLabel = "HkdFor"
type MirroredElemTypes = Tuple.Map[m.MirroredElemTypes, F]
type MirroredElemLabels = m.MirroredElemLabels
}) = Mirror.Product {
type Kind = K0.type // <------------ NEW
type MirroredType = HkdFor[T, F]
type MirroredMonoType = HkdFor[T, F]
type MirroredLabel = "HkdFor"
type MirroredElemTypes = Tuple.Map[m.MirroredElemTypes, F]
type MirroredElemLabels = m.MirroredElemLabels
override def fromProduct(p: Product): MirroredMonoType = ???
}
(^ equivalent to previous example except for the type Kind = K0.type)
This bug should be fixed in v3.4.2 of Shapeless 3, but it is not released yet.
Import Macros #
The last topic I want to touch on today is something I call “import macros”, named after a cool Pre-SIP that hasn’t made it to implementation yet. The trick isn’t necessary to implement our example usecase HkdFor but it is simply too useful not to explain here. The basic idea of the linked proposal is to have a new kind of macro that returns a list of Definitions and you would then be able to export it to add the definitions to a class:
def myMacro(using Quotes)(): List[quotes.reflect.Definition] = ???
class DecoratedClass {
export ${myMacro()}.* // adds publicly visible definitions to DecoratedClass
}
We can already do something similar with structural refinements to import a number of definitions into a scope:
class ImportMacroImpl extends Selectable {
def selectDynamic(name: String): Any = ???
def applyDynamic(name: String)(args: Any*): Any = ???
}
transparent inline def importMacro(): Any =
// this could be implemented by a macro
new ImportMacroImpl() {
val iVal: Int
def iDef(x: Int): Float
}
{
val i = importMacro()
import i.*
// use definitions created by the macro
val _: Int = ieVal
val _: Float = ieDef(1)
}
Unfortunately, export like in the SIP is not possible with structural refinements. You’ll have to use implicit conversions for that. Also, don’t forget that importMacro needs to be assigned to a temporary variable i before importing, as the path in an import-statement has to be a stable identifier.
Recap #
To summarize:
- We create a single implementation class to hold the runtime state (fields and methods) in an untyped map and runtime type information about erased type parameters.
- The implementation class is hidden behind an opaque type alias so that we can take advantage of
TypeTest. - By implementing the
scala.Dynamicinterface we gain the ability to resolve field and method accesses manually inside a macro. Dynamiconly provides type information after accessing a field/method and executing the macro. To provide type information in advance to the IDE for code completion, we write another macro that generates a structural refinement type within a given. An implicit conversion then decorates any instance of our target type with this structural refinement.<:<implicits may have to be given to establish subtype relationships between the abstract types if variance annotations are not enough- Because all the abstract types differ only in their erased type parameters,
TypeTestinstances andunapplyextractors have to be written to make pattern matching possible. - If exhaustion checking is desired, this has to be implemented either by casting the abstract type to an anonymous union of its children (if variance annotations are used for subtyping) or by implementing a custom match macro.
- We can provide implicit
Mirror.SumorMirror.Productinstances manually to make generic derivation in other libraries work with our abstract types.
Kommentare